Correlated stocks and Pair Trading
Pair Trading
이전 포스팅에서 correlated stocks에 대해 알아보았습니다.
이제 이 상관관계를 이용하여 간단한 페어 트레이딩전략을 이용해보겠습니다. 페어 트레이딩은 수학적 분석에 기반한 전략입니다.
여기서는 삼성전자와 그 계열사인 삼성전기를 예로 들겠습니다. 만약 삼성전자와 삼성전기가 같은 경제적 기반을 가지고 있다는 가정에서 우리는 이 두 종목의 가격의 차이(spread)혹은 비율이 시간이 지나도 일정하게 유지될 것을 기대할 것입니다. 그러나 삼성전자에 대해 대규모 매매주문, 뉴스에 대한 반응 등으로 인해 수시로 일시적인 수요/공급 변화가 생긴다면, 이 시나리오에서 삼성전자는 위/아래로 움직이고 삼성전기은 서로 다른 움직임을 보일 수 있습니다. 이 발산이 시간이 지남에 따라 정상으로 되돌아 갈 것으로 예상된다면 이 때 페어 트레이딩을 할 수가 있습니다.
Cointegration
공적분은 correlation과 매우 유사합니다. 두 series 간의 비율이 평균을 중심으로 달라짐을 의미합니다. 두 series Y, X는 다음과 같습니다.
Y = ⍺ X + e
여기서 ⍺는 상수 비율이고, e는 white noise입니다. 두 시계열 간의 페어 트레이딩이 동작하기 위해서는, 시간 경과에 따른 비율의 기대 값이 평균에 수렴되어야 합니다. 즉, 그들은 공적분되어야 합니다. 아래와 같은 형태가 cointegrated된 형태입니다.
Pair Trading을 하는 방법
다시 Y = ⍺ X + e 에서 본 X와 Y으로 돌아가면, Y/X와 같은 비율은 mean value ⍺ 에서 등락을 할 것입니다. 그렇기 때문에 우리는 X와 Y가 멀리 떨어질 때, ⍺가 너무 높거나 낮을 때를 포착하면 됩니다.
- Going Long the Ratio ⍺ 가 평소보다 작으며 증가할 것을 예측할 때, 우리는 Y를 사고 X를 파는 것에 배팅합니다.
- Going Short the Ratio ⍺가 평소보다 크고 감소할 것을 예측할 때의 경우입니다. 우리는 X를 사고 Y를 파는 것에 배팅합니다.
우리는 항상 "hedged postion"입니다. : 매도 포지션의 가치가 떨어지면 매수 포지션이 되고, 매수 포지션이 되면 매도 포지션으로 돈을 벌어 전체 시장 변동에 영향을 받지 않습니다. 종목 X와 Y가 서로 상대적으로 움직일 때만 수익을 얻거나 잃게 됩니다.
우리는 cointegrated할 것으로 생각되는 종목을 찾을 때 여러 비교 바이어스에 빠지게 됩니다.
- 다중 비교 편향 은 단순히 많은 테스트를 실행할 때 p 값을 잘못 생성할 기회가 증가한다는 사실입니다. 이를 피하기 위해, 공적분이 될 것으로 의심되는 이유가 있는 소수의 쌍을 선택하고 개별적으로 선택해야합니다. 이전 포스팅에서 상관관계가 있는 주식을 찾은 것과 관계가 있습니다.
이제 우리는 실제 종목에 적용시켜 두 종목간의 비율을 비교해보도록 하겠습니다. cointegration을 확인하기 위해 통계 패키지인 statsmodels을 이용합니다.
from statsmodels.tsa.stattools import coint
Data
데이터는 아래와 같이 date가 index이고 symbol이 column인 DataFrame을 이용할 것입니다.
Input :
data.head(3)
Output:
이제 이 데이터들을 이용하여 conitegrated된 쌍을 찾을 것입니다. 아래와 같이 함수를 정의한 뒤 사용합니다.
Input :
def find_cointegrated_pairs(data):
n = data.shape[1]
score_matrix = np.zeros((n, n))
pvalue_matrix = np.ones((n, n))
keys = data.keys()
pairs = []
for i in range(n):
for j in range(i+1, n):
S1 = data[keys[i]]
S2 = data[keys[j]]
result = coint(S1, S2)
score = result[0]
pvalue = result[1]
score_matrix[i, j] = score
pvalue_matrix[i, j] = pvalue
if pvalue < 0.02:
pairs.append((keys[i], keys[j]))
return score_matrix, pvalue_matrix, pairs
# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds,
yticklabels=instrumentIds, cmap=’RdYlGn_r’,
mask = (pvalues >= 0.98))
plt.show()
print(pairs)
Output:
[('000660', '071050'), ('016360', '066570'), ('016360', '005940'), ('016360', '012450'), ('066570', '005490'), ('066570', '005940'), ('006800', '003550'), ('006800', '012450'), ('003550', '004020'), ('003550', '086790'), ('003550', '024110'), ('003550', '003490'), ('003550', '042670'), ('005940', '012450'), ('005940', '042670'), ('055550', '024110'), ('086790', '051910'), ('086790', '028050'), ('086790', '012330'), ('086790', '096770'), ('000720', '042670')]
p-value가 0.02이하인 쌍만 추가한 결과, 위와 같은 결과가 나왔습니다. 삼성전자는 p-value가 0.02이하인 쌍이 없었으며 가장 p-value가 가장 낮은 쌍은 LG(003550)와 기업은행(024110) 이 나왔습니다. 이 두 종목으로 나머지 과정을 진행해보겠습니다.
결과로 나온 비율은 안정적으로 평균 주위에 맴도는 것처럼 보입니다. 하지만 통계적으로 절대 비율은 매우 유용하진 않습니다. 이 signal을 z-score로 normalize해보도록 하겠습니다.
Z Score (Value) = (Value — Mean) / Standard Deviation
주의
실제로 이것은 일반적으로 데이터에 scale을 하기위해 수행되지만 이것은 분포를 가정합니다. 대개 normal을 사용합니다. 그러나 많은 데이터가 normal distribution으로 되지 않으므로 이러한 분포를 사용할 때는 매우 조심해야 합니다. 비율의 실제 분포는 매우 극단적인 값으로 모델이 엉망이 되어 큰 손실을 초래할 수 있기 때문입니다.
Input :
def zscore(series):
return (series - series.mean()) / np.std(series)
zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()
Output :
우리는 이제 trading signal을 개발해보겠습니다. data techniques을 이용하여 trading singal을 개발하는 방법을 steps순으로 진행할 것입니다.
- 신뢰할 수 있는 데이터 수집 및 데이터 정리
- 거래 signal / logic을 식별하기 위해 데이터로부터 feature 생성
- feature는 MA혹은 가격 데이터, correlation또는 복잡한 signal의 ratio일 수 있습니다. 이를 결합하여 새로운 기능을 만들 수 있습니다.
- 이러한 기능을 사용하여 거래 signal을 생성합니다.
Step 1. 문제 설정
여기서 우리는 다음 순간이 매수 혹은 매도인지를 알려주는 신호를 만들겠습니다. 예측 변수 Y는
Y = Ratio is buy (1) or sell (-1)
Y(t)= Sign( Ratio(t+1) — Ratio(t) )
우리는 실제 주식 가격이나 비율의 실제 가치를 예측할 필요가 없다는 점에 유의하셔야 합니다.
Step 2. 신뢰할 수 있고 정확한 데이터 수집
거래하고자하는 주식과 사용할 데이터를 가져와 배당금과 액면 분할을 고려해줘야합니다.
Step 3. 데이터 분할
이전 포스팅에서 한 것처럼 training과 test셋을 각각 70%, 30%로 나눌 것입니다.
Step 4. Feature Engineering
우리는 ratio의 이동방향을 예측하려고 합니다. 우리는 두 주식이 공적분되면 비율이 평균으로 되돌아가는 경향이 있음을 보았습니다.
다음과 같은 기능을 사용합니다.
- ratio의 60일 이동 평균 : 이동 평균 측정
- ratio의 5일 이동 평균 : 평균의 현재가치 측정
- 60일 표준 편차
- z score : (5일 이동평균 - 60일 이동평균) / 60일 표준 편차
Input :
ratios_mavg5 = ratios.rolling(window=5,
center=False).mean()
ratios_mavg60 = ratios.rolling(window=60,
center=False).mean()
std_60 = ratios.rolling(window=60,
center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()
Output :
이번엔 이동 평균의 z-score ratio를 확인해보도록 하겠습니다.
Input :
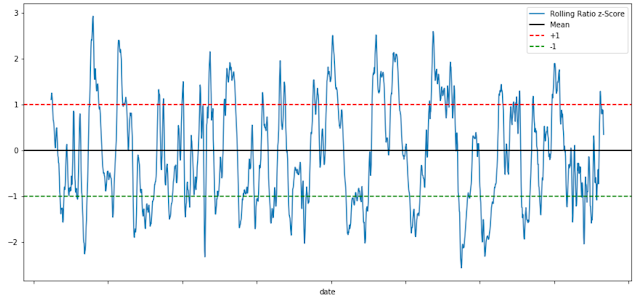
plt.figure(figsize=(15,7)) zscore_60_5.plot() plt.axhline(0, color='black') plt.axhline(1.0, color='red', linestyle='--') plt.axhline(-1.0, color='green', linestyle='--') plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1']) plt.show()
Output :
이동 평균의 z-score는 평균으로 회귀하는 정도가 매우 강한 것을 확인할 수 있습니다.
Step 5. 모델 선택
아주 간단한 모델부터 시작해보겠습니다. 우리는 z-score feature가 매우 높아지거나 매우 낮아질 때마다 회귀하는 것을 알 수 있습니다. +1 / -1을 threshold로 설정하여 trading signal을 생성하는 모델을 사용하도록 하겠습니다.
- Ratio는 z-score가 -1.0이하로 내려갈 때마다 buy (1) 신호를 생성합니다. 왜냐하면 z-score가 0으로 돌아가므로 ratio가 증가할 것이기 때문입니다.
- z-score가 1.0을 넘을 때 z-score가 0으로 내려가므로 ratio가 감소할 것이기 때문에 sell (-1) 신호를 생성합니다.
Step 6. 훈련
마지막으로, 우리의 모델이 실제 데이터에 잘 작동하는지 확인햅시다. 실제 ratio와 trading signal을 확인해 보도록 하겠습니다.
Input :
# Plot the ratios and buy and sell signals from z score plt.figure(figsize=(15,7)) train[60:].plot() buy = train.copy() sell = train.copy() buy[zscore_60_5>-1] = 0 sell[zscore_60_5<1 0="" atio="" buy="" color="’r’," ell="" linestyle="’None’," marker="’^’)" plot="" plt.axis="" plt.legend="" plt.show="" pre="" ratios.max="" ratios.min="" sell="" signal="" uy="" x1="" x2="" y1="" y2="plt.axis()">
Output :
signal들은 합리적으로 보입니다. 우리는 ratio가 높을 때 sell signal, 낮을 때 buy signal을 표시하고 있습니다.
이번엔 실제 종목들의 가격 변화와 signal들을 보도록 하겠습니다.
Input :
# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['LG','IBK', 'Buy Signal', 'Sell Signal'])
plt.show()
Output :
training data에 확인한 결과는 위와 같습니다. 이제 이 모델을 그대로 test data에 적용시켜 확인해보도록 하겠습니다.
Step 7. 테스트
z-score를 이용한 모델을 사용합니다. test data에서도 확인할 수 있듯이 ratio는 어떠한 상수를 기준으로 위아래로 등락하는 것을 확인할 수 있습니다. (여기서는 약 5.5), z-score가 1을 초과할 때 sell signal을 보내고, -1미만일 때 buy signal을 보내고 있습니다.
아래의 그림은 종목들의 주가와 같이 확인한 결과입니다. 오히려 전체적으로 가격이 상승하는 국면에서는 sell signal이 많이 발생하고, 하락하는 국면에서 buy signal이 발생하고 있습니다.
이번 포스팅에서는 모델 validation과 backtest 과정은 생략하겠습니다. 전체적인 과정을 설명하기 위해 아주 단순한 방법으로 상관관계를 갖는 종목을 이용한 pair trading signal 발생을 해보았습니다. 여기서는 간단한 방식으로 5d-MA와 60d-MA만을 이용해 signal을 이용해보았지만, 본인의 trading 전략을 세운 뒤에 이용한다면 alpha를 찾아낼 수 있는 기회를 포착할 수 있을 것입니다. 어도비와 마이크로소프트와 같이 강력한 cointegration을 가지고 있는 종목들이 발견되지 않는다면, 선물, 옵션, ETF등과 같은 여러 방법을 이용하면 상관관계를 포착할 수 있을 것입니다.
















유익한 정보 감사합니다. 혹시 Z Score (Value) = (Value — Mean) / Standard Deviation, standard deviation이 표준편차라면 공식에서 value와 mean가 뜻하는게 뭔지 알 수 있을요?
답글삭제